오늘 파일처리 첫수업에서 교수님께서 갑자기 이산수학 이야기를 끄집어 내셔서 결국 파일처리가 어떤 과목인가 보다는 이산수학2 수업이 되어 버렸다. (어쩌면 오토마타2인가.. -_-;; 자료구조2?) 먼가 이 내용이 비둘기집의 원리에서부터 출발하였는데... 왜!!!!!! ;;;;;;;;;;; 당췌 모를일이다...
이번학기 첫번째 과제중의 대각선법에 대한 내용이다.
- 이때의 비가산집합이라는 것은 자연수의 성질 중 하나인 countable의 반대되는개념으로 비가산집합이라는 말을 쓴다. (countable은 무한 하지만 셀수있는 - 실제로 수직선상에 표현을 하자면 일정한 간격을 가지고 존재하므로 어떤 임의의 수를 선택한다면 그 수에 일정간격을 더하거나 빼었을때 그 자리에 항상 같은 집합에 속하는 수가 존재하게 된다.)
- 칸토어의 대각선법(Cantor's diagonal method)를 이용해 이것을 증명할 수 있다.
- 실수의 부분 집합인 단위 개구간 (0,1)사이의 모든 실수의 집합이 비가산임을 보여, 정체 실수의 집합 또한 비가산임을 증명한다.
(수업시간에는 폐구간 [0, 1] 사이의 모든 실수의 집합이 비가산임을 보이고 폐구간 [0, 100] 또한 비가산임을 증명하였다.)
0과 1 사이의 모든 실수의 집합이 가산이라고 가정하자. (countable)
그러면 이러한 수둘의 10진법 표현은 다음과 같은 리스트로 나타낼 수 있다.
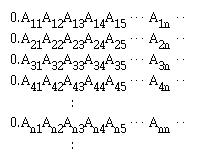 양의 정수 쌍 i와 j에 대하여, 이 리스트에서 i번째 수의 j번째 10진수는 Aij이다. 즉 첫 번째 수의 첫 번째 10진 숫자는 A11이고, 두번째 10진수는 A22등이다. 예를 들면 0과 1 사이의 실수 리스트가 다음과 같이 시작한다고 가정하자.
양의 정수 쌍 i와 j에 대하여, 이 리스트에서 i번째 수의 j번째 10진수는 Aij이다. 즉 첫 번째 수의 첫 번째 10진 숫자는 A11이고, 두번째 10진수는 A22등이다. 예를 들면 0과 1 사이의 실수 리스트가 다음과 같이 시작한다고 가정하자.
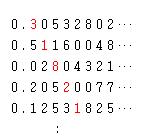 대각선에 위치한 원소들을 붉은색으로 표시하였는데
대각선에 위치한 원소들을 붉은색으로 표시하였는데
이 대각선에 있는 원소들을 하나씩 보면서 각각 원래의 숫자가 아닌 다른 숫자로 된 새로운 십진수 B를 만들 수 있다. 예를 든다면 0.23712.. 이던가 0.12313.. 이런 수를 만들 수 있을 것이다. 여기에서 B=0.23712..으로 잡는다면 위의 리스트에 나와있는 수와 비교를 했을 때 반드시 n번째 리스트에 있는 실수는 소수점이하 n번째 자리에서 B와 다른 수를 가지므로 B는 리스트에 포함되지 않는 수임을 알 수 있다. 그러나 B는 역시 0과 1 사이의 수이면서 리스트에 빠져있기때문에 가산이라는 가정에 모순이 생긴다.
따라서, 0과 1 사이의 모든 실수는 비가산이다.
오토마타시간에 배운 내용은 아마 이진법으로 되어있던 n*n행렬이었던것 같은데...............? -_-;;;
기억이... 기억이..... 학교가서 다시 책을 찾아봐야겠다.. 그때는 0 또는 1로 되어 있어서 matrix의 대각선을 0은 1로 1은 0으로 바꾸어서 만든 수였나..;;
사실 대각선법 그러니깐... 그게 머야 배웠더냐 라는 생각이었는데.. 음... 다시 보니 기억이 나는군 비가산이 머지... 이런생각 한 3.4초쯤 해주고.. 아하! 이래 떠올라서 다행이넵 ㅋㅋ
-> 기본 내용은 http://blog.naver.com/pupleshiner 에서 퍼온 내용입니다.
두번째 문제를 푸는데에 있어서 중요한 단서가 되는 내용이라고 하니 일단은 생각을 해둬야겠습니다. ㅋㅋㅋ 난 x와 y의 일대일대응의 관계에만 치우쳐 생각을 했지만.. 이제 대각선법을~!!!
이래봤자 머 모르겠노..ㅠ
이번학기 첫번째 과제중의 대각선법에 대한 내용이다.
[증명] 실수의 집합은 비가산집합이다. (칸토어의 대각선법)
- 이때의 비가산집합이라는 것은 자연수의 성질 중 하나인 countable의 반대되는개념으로 비가산집합이라는 말을 쓴다. (countable은 무한 하지만 셀수있는 - 실제로 수직선상에 표현을 하자면 일정한 간격을 가지고 존재하므로 어떤 임의의 수를 선택한다면 그 수에 일정간격을 더하거나 빼었을때 그 자리에 항상 같은 집합에 속하는 수가 존재하게 된다.)
- 칸토어의 대각선법(Cantor's diagonal method)를 이용해 이것을 증명할 수 있다.
- 실수의 부분 집합인 단위 개구간 (0,1)사이의 모든 실수의 집합이 비가산임을 보여, 정체 실수의 집합 또한 비가산임을 증명한다.
(수업시간에는 폐구간 [0, 1] 사이의 모든 실수의 집합이 비가산임을 보이고 폐구간 [0, 100] 또한 비가산임을 증명하였다.)
0과 1 사이의 모든 실수의 집합이 가산이라고 가정하자. (countable)
그러면 이러한 수둘의 10진법 표현은 다음과 같은 리스트로 나타낼 수 있다.
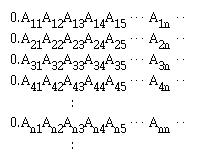
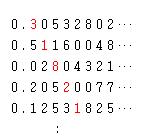
이 대각선에 있는 원소들을 하나씩 보면서 각각 원래의 숫자가 아닌 다른 숫자로 된 새로운 십진수 B를 만들 수 있다. 예를 든다면 0.23712.. 이던가 0.12313.. 이런 수를 만들 수 있을 것이다. 여기에서 B=0.23712..으로 잡는다면 위의 리스트에 나와있는 수와 비교를 했을 때 반드시 n번째 리스트에 있는 실수는 소수점이하 n번째 자리에서 B와 다른 수를 가지므로 B는 리스트에 포함되지 않는 수임을 알 수 있다. 그러나 B는 역시 0과 1 사이의 수이면서 리스트에 빠져있기때문에 가산이라는 가정에 모순이 생긴다.
따라서, 0과 1 사이의 모든 실수는 비가산이다.
오토마타시간에 배운 내용은 아마 이진법으로 되어있던 n*n행렬이었던것 같은데...............? -_-;;;
기억이... 기억이..... 학교가서 다시 책을 찾아봐야겠다.. 그때는 0 또는 1로 되어 있어서 matrix의 대각선을 0은 1로 1은 0으로 바꾸어서 만든 수였나..;;
사실 대각선법 그러니깐... 그게 머야 배웠더냐 라는 생각이었는데.. 음... 다시 보니 기억이 나는군 비가산이 머지... 이런생각 한 3.4초쯤 해주고.. 아하! 이래 떠올라서 다행이넵 ㅋㅋ
-> 기본 내용은 http://blog.naver.com/pupleshiner 에서 퍼온 내용입니다.
두번째 문제를 푸는데에 있어서 중요한 단서가 되는 내용이라고 하니 일단은 생각을 해둬야겠습니다. ㅋㅋㅋ 난 x와 y의 일대일대응의 관계에만 치우쳐 생각을 했지만.. 이제 대각선법을~!!!
이래봤자 머 모르겠노..ㅠ
